ACM ICPC 대비 문제 및 해설
글 제목은 ACM ICPC 대비 문제 및 해설인데 이 블로그 글에서는
이 대회가 무엇인지? 왜 이것을 공부해야하는지? 효과적 방법은 무엇인지? 에 대해 다룬다.
먼저 이 대회가 무엇인지는 라엘이가 작성한 다음의 글을 참조하여라.
ACM-ICPC 대회소개 및 참가조건, 규칙들 <- 클릭
프로그래밍을 배울 때, 우리는 일반적으로 다음의 순서를 따른다.
화면에 문자열 출력해 보기.
1) “Hello World” 화면에 출력하기
변수를 사용자로부터 입력받고 사용하기.
2) “Hi 홍길동! nice to meet you 표시하기”
제어문을 사용하여 1 부터 10까지 표시하기.
3) 1~ 100 까지 화면에 출력하시오
제어문과 연산자를 사용하기.
4) 구구단을 출력하시오
일상생활에 문제를 응용해보기 (제어문, 반복문, 변수개념)
5) 최대 100만원까지만 예금할 수 있고 1000원 단위로 입출금이 가능한 은행 프로그램을 제작하시오
+보통 일상생활에 적용할 줄 아는 5번까지 되면 “프로그래밍을 할 줄 안다” 라고 한다.
알고리즘을 적용해서 풀어보기.
6) 임의의 100개의 정수를 입력받아서 오름차순으로 정렬한 후 출력하시오.
알고리즘을 적용해서 풀어보기. (이건 좀 ICPC 수준의 어려운 문제이다. 아마 당신은 이것을 못풀것이다.)
7) 한국의 각 도시에 다음과 같은 도로가 있다. 도로간의 거리는 다음과 같다.
임의의 두 도시를 선택했을 때 그 도시간의 최단거리를 구하여라.
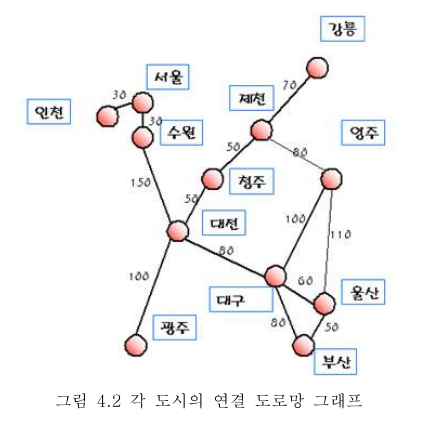
+7번까지 할 줄 알면 “프로그래밍 더 할 줄 안다” 가 된다.
7번 정도까지 풀 줄 알면 프로그래밍을 배우는 학생이 자만에 빠질 수 있는데 이 자만 단계의 사람에게 채찍질을 할 용도로 ACM ICPC 문제가 사용되곤 한다.
일반적으로 ICPC문제는 깊은 사고력이 있어야 겨우 풀수 있는 문제들이다.
하지만, 문제를 풀 수 있다고 해서 능력있는 개발자라는 말은 하지 말도록 하자.
내 생각에 아이폰이 등장한 2009년 이후로
과거의 “문제만 풀리면 통과되던”시대가 아니라, 효율을 따지는 시대가 되었다.
IT에서의 주도권이 하드웨어에서 소프트웨어로 이동한 것이다.
(IT 분야에서만이 아니라 모든 분야에서 소프트웨어 혁명이 일어났다)
(검색 서비스로 시작한 구글이 엄청난 수의 공장을 보유한 모토롤라를 인수했고,
운영체제 제작회사 MS가 노키아라는 회사를 인수했다.
라엘이는 이러한 것은 별로 와 닿지 않고 얼마전이 이 기사가 와닿았다.)
뉴스 보도자료를 쉽게 풀어서 쓰자면 투자자들이 페이스북을 IBM보다 더 가치있는 회사라고 생각하는 것이다.
아무튼 요즘의 화두는 A라는 일을 해결하는데
속도를 더 빠르게 하기 위해서 하드웨어를 업그레이드 하는 것이 아니라 소프트웨어를 업그레이드 하는 것이다.
하드웨어는 돈을 2배를 소비해서 업그레이드 해 봤자 10%~30% 효율 상승밖에 없다.
반면에 소프트웨어는 업그레이드시 0%~수만% 까지 효율 개선이 일어날 수 있다.
낮은 가격, 저전력 이라는 시대의 요구에 따라서 우리는 효율적으로 프로그래밍을 해야 한다.
효율적인 프로그래밍이란 더 낮은 노력으로 더 나은 결과를 얻는 것이다.
1) 요즘같은 스마트 시대에 효율적인 프로그래밍을 하면
CPU 계산 횟수가 낮아지고, 발열이 낮아지고, 배터리가 오래가며, 속도가 빨라진다.
2) 요즘같이 데이터가 쌓이고 쌓인 빅데이터 시대에 효율적인 프로그래밍을 하면
수많은 자료(data)에서 진귀한 정보(valuable information)를 쉽게 얻어 낼 수 있다.
즉 요즘 시대의 경쟁력 있는 개발자가 되기 위해서 ICPC 문제를 풀어보고 생각해 보아야 한다.
문제 풀이에 들어가기에 앞서 컴퓨터 공학 개념 한가지를 알고 가자.
- 알고리즘의 성능평가
1) 공간 복잡도 : 알고리즘을 수행하는데 사용되는 공간을 평가한다.
2) 시간 복잡도 : 알고리즘이 몇회 수행되는지 연산의 횟수를 평가한다.
공간 복잡도는 알고리즘을 푸는데 사용되는 공간의 양으로 그 알고리즘의 성능을 평가하는 것이다.
요즘 시대에 지속적인 하드웨어의 가격하락으로 인해 (14년 현재 초등학생이 쓰는 PC도 램이 8GB~16GB가 장착되더라) 거의 무제한(제한 없는) 공간을 사용할 수 있게 되었다. 따라서 공간 복잡도는 알고리즘 성능 평가에서 잘 사용되지 않는다.
공간을 더 쓰더라도 시간만 단축되면 더 효율적인 알고리즘이 되는 것이다.
주로 시간 복잡도로 알고리즘의 성능을 평가하는데 ,
시간 측정의 경우 하드웨어의 특성에 따라서 달라지게 되고
반복 횟수를 측정하는 경우 변수 n에 의해서 횟수가 달라지게 된다.(변수는 더 많을 수도 있고, rand 나 time 같은 것일 수도 있다.)
알고리즘의 최대, 최소, 평균 수행횟수 등을 측정하는 방법도 있다.
아무튼 시간 복잡도를 측정하는 여러 방식이 있으나 측정의 어려움 때문에 주로 점근 표기법을 사용한다.
점근 표기법이란 간단히 말해서 “대략적인 시간소요” 를 말한다. A 알고리즘은 B 알고리즘에 비해 2배 빨라! 같은 정확한 성능비교가 아니다!
3) 점근 표기법 : 시간 복잡도 계산이 어려우므로 알고리즘의 성능을 평가할 용도로 대략적인 시간 복잡도를 표기하는 방법이다.
여러가지 점근 표기법 중에서 빅 오 표기법이 주로 사용되니 빅 오 표기법만 살펴보자.
빅 오 표기법이란 O(n) 이라고 쓰는 것이다.
오O 를 쓰고 괄호에 대략적인 시간 복잡도를 표시한다.
정의 : f와 g를 각각 0보다 큰 정수 n에 대한 함수라 하자. 이때 모든 n(n ≥ m)에 대해 f(n) ≤ cg(n)을 만족시키는 m과 c가 모두 존재하면 f(n) = Ο(g(n))이다
간단히 말해서 가장 높은 차수만 고려하는 것이다.
입력 변수 n 에 대해서 알고리즘의 반복 횟수를 계산하니 다음과 같을 때 빅 오 표기법으로 표시하면 다음과 같다.
n^2 + 4n + 6 => O(n^2)
30n^2 + 1 => O(n^2)
45n + 20n + 100n => O(n)
40 => O(1)
>> 이 경우 비록 n 이 미지수지만 성능평가를 해보자면 “4번째가 가장 빠르고, 3번째가 그다음 빠르고 , 첫번째 및 두번째는 비슷하다” 라고 말할 수 있다.
변수 n에 대하여 두 알고리즘의 시간복잡도를 계산 했을 때
하나가 1000n + 500 의 시간 복잡도가 있고
다른 하나가 n^2 + 1 의 시간 복잡도가 있을 때
n이 2라고 입력되면
첫번째 알고리즘은 2500회 연산되고, 두번째 알고리즘은 5회 연산된다. 두번째 알고리즘이 더 효율적으로 보인다.
하지만 점근표기법 중 빅오 표기법으로 나타내면
1000n + 500 = O(n)
n^2 + 1 = O(n^2)
이 되고 첫번째 알고리즘이 효율적이 된다.
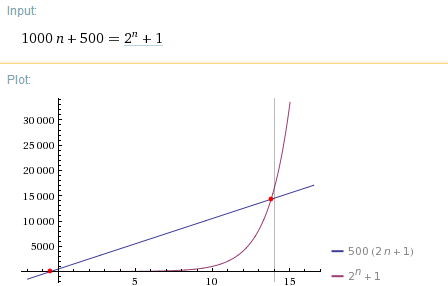
그래프 계산 : (온라인 알고리즘 계산기 wolfram alpha) http://www.wolframalpha.com/input/?i=1000n%2B500%3D2%5En%2B1&dataset=
미지수 n에 대해서 그래프를 그려 살펴 보자면 위와 같이 n이 14이상이 되면 두번째 알고리즘의 수행횟수가 엄청나게 증가하는 것을 볼 수 있다.
이런 이유로 첫번째 알고리즘이 더 효율적이다! 라고 말할 수 있는 것이다.
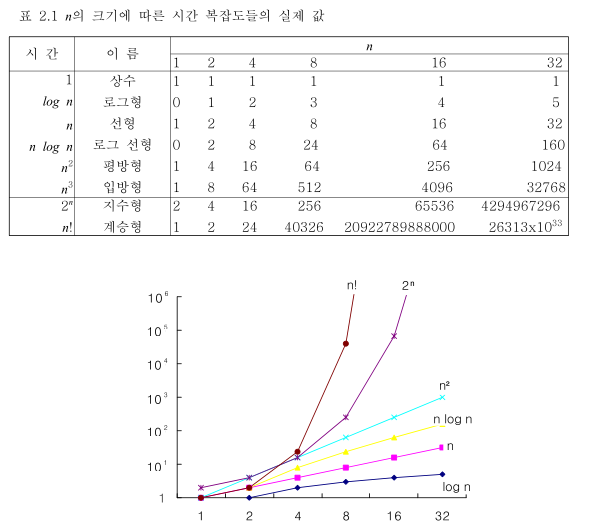
점근 표시법에서 다음과 같은 복잡도 서열이 있다.
낮은 서열(왼쪽)의 알고리즘 일 수록 좋다.(빠르다.=수행 횟수가 적다.)
![]()
자. 서론은 마치고 이제 실제 문제를 살펴 보도록 하자.
우리가 살펴볼 문제는 2012년 한국 대회 지역예선 문제 중 하나이다.
![]() AllProblems.pdf
AllProblems.pdf
이 문제는 ACM KAIST 홈페이지에서도 다운받아 볼 수 있다. (http://acm.kaist.ac.kr/phpBB3/portal.php 홈페이지가 심각하게 불편하게 만들어져 있으므로 잘 찾아보길 바란다.)
B 번 문제를 살펴보자.
한글로 변역해서 보도록 하겠다.
Canoe Racer
카누 선수
국제 카누대회가 근 시일에 열릴 예정이다. 국제 카누대회에서 사용되는 공인된 경기용 배로는
C1, C2, 그리고 C4가 있다; C는 카누를 나타내고 숫자는 노를 젓는 사람수를 나타낸다. 국제대회에서는
200m, 500m, 그리고 1000m 종목에서 경기를 치른다.
대한체육학교는 국제 카누경기 종목 중에서 C4 1000m 종목에 출전할 예정이다. 대한체육학교에는 같은
학생수를 가진 네 개의 반이 있어서 각 반에서 한 명씩의 선수를 선발 하려고 한다. 대한체육학교는 많은
C4 경기용 배를 가지고 있는데 각각의 배들은 네 선수의 무게 합이 특정 값에 가까울수록 더 좋은 성능을
발휘한다. 예를 들어, 한 배의 특정 값이 300이고 네 반 학생들의 무게가 다음과 같다고 하자.
1반: 60, 52, 80, 40
2반: 75, 68, 88, 63
3반: 48, 93, 48, 54
4반: 56, 73, 49, 75
위의 경우에는 각 반에서 무게가 60, 75, 93, 73 인 학생 들을 선발하면 네 학생의 무게 합이 301이어서
300과 가장 가까우므로 그 배에 제일 적합한 선수들이다. 어떤 경우에는 특정 값에 가장 가까운 무게 합이
두 개일 때가 있다. 예를 들면 어떤 배의 특정 값이 200이고 이에 가장 가까운 무게 합이 198과 202인 경우를 보자.
그런 경우에는 무게 합이 작은 쪽이 카누 경기에 유리하다. 그러므로 무게 합이 198인 네 학생들이 선발되어야 한다.
배의 특정 값과 네 반 학생들의 무게가 주어졌을 때, 위의 조건을 만족하는 네 선수를 선발하는 프로그램을 작성하시오.
[입력 형식]
입력은 표준입력으로부터 읽으시오. 입력은 T 개의 테스트케이스로 이루어져 있다. 테스트케이스 수 T가
입력의 첫 줄에 주어진다. 각 테스트케이스의 첫 줄에는 두 개의 정수 k 와 n이 주어진다.
k 는 배의 특정 값을 나타내고 n은 각 반의 학생 수를 나타낸다, 1≤k≤40,000,000, 1≤n≤1,000. 그 다음 네 줄에는
각 반의 학생들의 무게를 나타내는 정수들이 n 개씩 주어진다. 각 무게는 1 이상이고 10,000,000 이하이다.
[출력 형식]
출력은 표준출력을 사용하시오. 각 테스트케이스에 대해 한 줄을 출력하시오.
그 줄에는 카누 선수로 선발된 네 선수의 무게 합을 나타내는 정수를 출력하여야 한다.
[입출력 예]
| 입력 (stdin) | 출력 (stdout) |
| 3
300 4 60 52 80 40 75 68 88 63 48 93 48 54 56 73 49 75 8 3 1 2 3 1 2 3 1 2 3 1 2 3 32 2 2 5 9 4 10 20 4 2 |
301
8 31 |
해설(답을 나타내지는 않음) :
모든 경우의 수를 표시할 경우 한 팀당 N명이 있기 때문에 O(N^4) 복잡도가 생긴다.
n이 1000 인 경우 n^4 은 1000000000000(1조) 이므로 절대 제한시간(3초)안에 풀 수 없다.
우리는 제한 시간 안에 답을 구할 수 없으면 틀린 답으로 처리한다.
문제를 한단계 축약시킨 아래의 문제를 풀어보아라.
![]() acm_canoe.pdf
acm_canoe.pdf
문제 해결 샘플 소스 (틀만 있고 답은 없음)
import java.io.*;
public class Canoe {
static int solveCanoe(int k, int[] men, int[] women){
Arrays.sort(women);
/*
something..
*/
return closest;
}
public static void main(String[] args){
try {
Scanner sc = new Scanner(new File("src/canoe/canoe_input.txt"));
int T = sc.nextInt(); //testcase cnt
for(int t = 0;t<T;t++){
int k = sc.nextInt(); //target weight of boat
int n = sc.nextInt(); //number of people
//read data
int[] men = new int[n];
int[] women = new int[n];
for(int i=0;i<men.length;i++){
men[i] = sc.nextInt();
}
for(int i=0;i<women.length;i++){
women[i] = sc.nextInt();
}
System.out.println(solveCanoe(k,men,women));
}
sc.close();
}
catch (FileNotFoundException e){
e.printStackTrace();
}
}
}
테스트 데이터
![]() canoe_input.zip
canoe_input.zip
테스트 데이터에 대한 정답
![]() answer.txt
answer.txt
힌트 : 최적값을 찾기 위해서 우리는 효율적인 탐색 알고리즘을 사용해야 한다.
정렬하는데에는 그리 많은 노력(시간)이 들지 않는다.
정렬된 데이터가 있다면 binary search(이진 탐색) 기법을 사용하면 매우 빠른 시간에 원하는 값을 찾을 수 있다.
N개의 데이터에 대해서 평균적으로 LogN 번만에 찾아낼 수 있다.
1024개의 데이터가 있다면 평균적으로 Log1024 = 10 번만에 찾아낼 수 있다.
이것은 N 번을 검색하는 순차탐색에 비해서 매우 빠르다.
순차탐색 : 최악의 경우 N, 평균적인 경우 N/2
이 문제를 풀면 알겠지만 ICPC 문제들은
단순하고 쉽게 쓰여진 노가다 작업을
효율적인 알고리즘을 사용하여 노력(시간)을 단축시키는 켜야 하는 문제들이다.
대회에서 좋은 성과 있기를 바랍니다.
Good Luck to you!
